Convolutions

Convolutions and convolutional neural network

Adapted from:

dsd = load_dataset("mnist")
trn, tst = dsd["train"], dsd["test"]
xb = T.to_tensor(trn[0]["image"])[None, ...]
xb.shape
torch.Size([1, 1, 28, 28])

This is a nice resource.

Convolutions encode position equivariance like the probability that there is a bird at any particular location in an image. It’s implemented as a sliding matrix multiplication, followed by a sum like so:

kernel = tensor([[-1, -1, -1], [0, 0, 0], [1, 1, 1]])


def apply_kernel(row, col, img, kernel):
    # Normally, you would need to check if the kernel has
    # an odd or even size
    width, height = kernel.shape
    receptive_field = img[
        row - (height // 2) : row + (height // 2) + 1,
        col - (width // 2) : col + (width // 2) + 1,
    ]
    return (receptive_field * kernel).sum()


*_, w, h = xb.shape
processed = [
    [apply_kernel(i, j, xb.squeeze(), kernel) for j in range(1, w - 1)]
    for i in range(1, h - 1)
]
processed = tensor(processed)

show_images(
    [kernel, xb.squeeze(), processed],
    titles=["Kernel", "Original", "Original + Kernel"],
    figsize=(8, 8),
);

You can see it is very easy to think of interesting features of images that are just convolutional filters.

One clever way of implementing this is the im2col algorithm that represents a convolution as a matrix multiplication and take advantage of highly efficient algorithms for matrix multiplications. It does so by unrolling the input matrix matrix such that every receptive field is a contiguous block of values, with a correspondingly unrolled contiguous block of convolutional filter values. The values of the convolutional matrix can change, but they are shared.

This has a corresponding function in PyTorch.

F.unfold?
Signature:
F.unfold(
    input: torch.Tensor,
    kernel_size: None,
    dilation: None = 1,
    padding: None = 0,
    stride: None = 1,
) -> torch.Tensor
Docstring:
Extracts sliding local blocks from a batched input tensor.
.. warning::
    Currently, only 4-D input tensors (batched image-like tensors) are
    supported.
.. warning::
    More than one element of the unfolded tensor may refer to a single
    memory location. As a result, in-place operations (especially ones that
    are vectorized) may result in incorrect behavior. If you need to write
    to the tensor, please clone it first.
See :class:`torch.nn.Unfold` for details
File:      ~/micromamba/envs/slowai/lib/python3.11/site-packages/torch/nn/functional.py
Type:      function
# Need to add a channel dimension and a batch dimension
xb_unfolded = F.unfold(xb, kernel_size=(3, 3)).float()
kernel_unfolded = kernel.view(-1).float()

# im2col
xb_processed = kernel_unfolded @ xb_unfolded

# Reshape
xb_processed = xb_processed.view(26, 26)
show_image(xb_processed);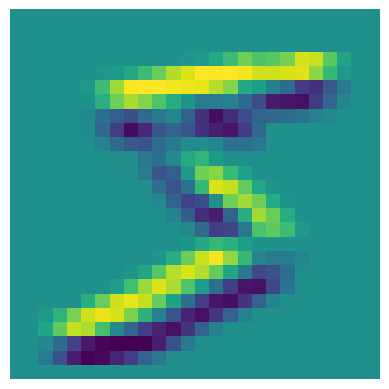

This unfold trick is about the same efficiency as the built-in convolution layer.

For better performance, we can apply a bunch of convolutions simultaneously.

diag1_edge = tensor([[0, -1, 1], [-1, 1, 0], [1, 0, 0]]).float()
diag2_edge = tensor([[1, -1, 0], [0, 1, -1], [0, 0, 1]]).float()
left_edge = tensor([[-1, 0, 1], [-1, 0, 1], [-1, 0, 1]]).float()

edge_kernels = torch.stack([left_edge, diag1_edge, diag2_edge])
edge_kernels.shape
torch.Size([3, 3, 3])
batch_features = F.conv2d(xb, edge_kernels[:, None, ...])
show_images([batch_features[0, i] for i in range(3)])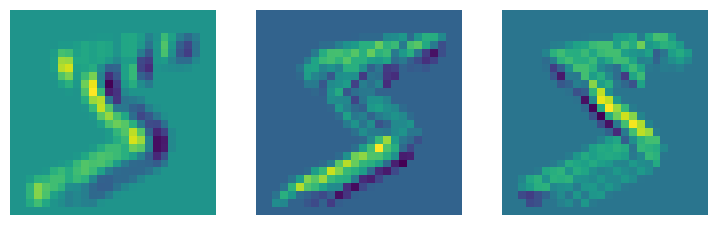

The parameters to a convolutional layer are the stride and padding, which allow us to manipulate the size of the feature map.

Creating a CNN

For classifying digits, we cannot solely use convolutional layers because it gives 10 outputs per pixel!

nh, n_outputs = 30, 10

partial_model = torch.nn.Sequential(
    torch.nn.Conv2d(1, 30, kernel_size=3, padding=1),
    torch.nn.ReLU(),
    torch.nn.Conv2d(30, 10, kernel_size=3, padding=1),
)

partial_model(xb).shape
torch.Size([1, 10, 28, 28])

Instead, we’ll add a lot of layers and chew up the extra feature map dimensions until we have a 1x1x10 feature map.

We’ll add a convenience function to create conv layers with optional activations.

source

conv

 conv (ni, nf, ks=3, stride=2, act=True)

We also need some annoying device stuff.

source

to_device

 to_device (x, device='cpu')

Now, define the model…

Note here that the default stride is 2, such that the feature map is downsampled by 2 each layer.

source

get_model

 get_model ()
get_model()

And we can train! 🏋️

source

get_dls_from_dataset_dict

 get_dls_from_dataset_dict (dsd, collate_fn=<function default_collate>,
                            bs=32)

source

fit

 fit (epochs, model, loss_func, opt, train_dl, valid_dl, tqdm_=False)

source

accuracy

 accuracy (y, y_pred)

source

fashion_mnist

 fashion_mnist (bs=256)

source

fashion_collate

 fashion_collate (examples)
model = get_model()
with fashion_mnist() as dls:
    fit(6, model, F.cross_entropy, optim.SGD(model.parameters(), lr=0.1), *dls)
epoch=0, validation loss=1.041, validation accuracy=0.62
epoch=1, validation loss=0.767, validation accuracy=0.73
epoch=2, validation loss=0.623, validation accuracy=0.78
epoch=3, validation loss=0.561, validation accuracy=0.80
epoch=4, validation loss=0.515, validation accuracy=0.81
epoch=5, validation loss=0.483, validation accuracy=0.82

This gives us comparable accuracy to the linear model, which had 39,760 parameters. In contrast…

sum(p.numel() for p in model.parameters())
5274

More tips:

  • Chewing up the feature map until we have one logit per dimension is not the only way to summarize the features before a classification/regression head. We can also use a dense layer or global average pooling
  • The receptive field of a convolution grows through the network, as the convolutions are functions of convolutions. Really nice illustration of that here