Predicting \(t\) as a function of \(x_t\)

Visually, it’s easy to distingush between noisy and noise-less images. Beforehand, we defined \(\epsilon_{\theta}^{(t)} (x_t, t)\) This module asks whether it is neccesary to pass \(t\) to the model at all; can the model figure it out itself?

Adapted from

aesthetics()

We need to be empirical and understand the success conditions. We need to know if our model is good – or if its even better than random!

Note that, to use our training loop, our torch modules need at least one trainable parameter and a trainable output.

class Dummy(nn.Module):
    def __init__(self):
        super().__init__()
        # We must have at least one parameter
        self._ = nn.Linear(1, 1)

    def forward(self, x_t):
        bs, *_ = x_t.shape
        # We must always output a trainable parameter
        return torch.full((bs,), 0.5, device=x_t.device, requires_grad=True)

Let’s define our dataset.

preprocess_ = torchvision.transforms.Compose(pipe)
def preprocess(examples):
    x_0 = [preprocess_(img) for img in examples["image"]]
    x_0 = torch.stack(x_0)
    ((x_t, t), _) = noisify(x_0)
    return {"x_t": x_t, "t": t.float()}
def get_dls(bs=512):
    dsd = load_dataset("fashion_mnist")
    dsd["train"].set_transform(preprocess)
    dsd["test"] = (
        dsd["test"]
        .map(preprocess, batched=True, remove_columns=["image", "label"])
        .with_format("torch")
    )
    return DataLoaders.from_dsd(dsd, bs=bs).listify(["x_t", "t"])

This was a bit annoying to set up, I had to learn the following:

test = load_dataset("fashion_mnist")["test"]
ptest = test.map(preprocess, batched=True)
xb = ptest[:2]["x_t"]
cxb = default_collate(xb)
assert type(cxb) == type(cxb[0]) == type(cxb[0][0]) == list
print(f"inner most type: {type(cxb[0][0][0])}")
print(f"shape: {len(cxb), len(cxb[0]), len(cxb[0][0]), cxb[0][0][0].shape}")
inner most type: <class 'torch.Tensor'>
shape: (1, 32, 32, torch.Size([2]))

To fix this, we need to convert arrow to torch before sending the batch to the collate function by adding .with_format("torch") like so:

xb = ptest.with_format("torch")[:2]["x_t"]
xb.shape
torch.Size([2, 1, 32, 32])

This is what it looks like:

dls = get_dls()
CPU times: user 2.23 s, sys: 229 ms, total: 2.46 s
Wall time: 2.73 s
r = dls.splits["test"][96]
xt, t = r["x_t"], r["t"]
show_images(xt, titles=[t])

(xb, t) = dls.peek()
n = 8
show_images(
    xb[:n].squeeze(),
    titles=[f"{tt.item():.2f}" for tt in t[:n]],
)

Now, we can train the dummy model.

def train(model, dls, n_epochs=20, lr=1e-2, log_periodicity=10, extra_cbs=None):
    T_max = len(dls["train"]) * n_epochs
    scheduler = BatchSchedulerCB(lr_scheduler.OneCycleLR, max_lr=lr, total_steps=T_max)
    cbs = [
        DeviceCB(),
        MetricsCB(),
        ProgressCB(plot=True, periodicity=log_periodicity),
        scheduler,
    ]
    if extra_cbs:
        cbs.extend(extra_cbs)
    learner = TrainLearner(model, dls, cbs=cbs)
    learner.fit(n_epochs=n_epochs)
train(Dummy(), dls, n_epochs=3)
loss epoch train
0.083 0 train
0.083 0 eval
0.083 1 train
0.083 1 eval
0.083 2 train
0.083 2 eval 

CPU times: user 3.94 s, sys: 1.82 s, total: 5.76 s
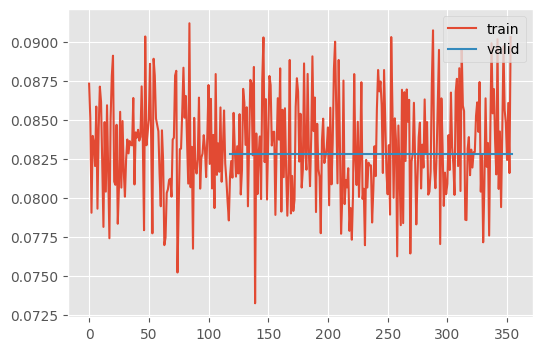
Wall time: 11 s

Notice that loss does not change during the second epoch. (It does change a tiny bit, for whatever reason.) This is our baseline. Anything worse than this is totally useless.

We can use the same model for classification from before, just changing the number of outputs and flattening it.

class RegressionResNet(ResNetWithGlobalPoolingInitialConv):
    def __init__(self, nfs=[16, 32, 64, 128, 256, 512]):
        return super().__init__(nfs, 1)

    def forward(self, x):
        x = super().forward(x)
        assert x.shape[-1] == 1
        return x.squeeze()
t_predictor = RegressionResNet.kaiming()
summarize(t_predictor, "ResidualConvBlock|Linear")
train(t_predictor, dls, n_epochs=5)
Type Input Output N. params MFlops
ResidualConvBlock (8, 16, 28, 28) (8, 32, 14, 14) 14,496 2.8
ResidualConvBlock (8, 32, 14, 14) (8, 64, 7, 7) 57,664 2.8
ResidualConvBlock (8, 64, 7, 7) (8, 128, 4, 4) 230,016 3.7
ResidualConvBlock (8, 128, 4, 4) (8, 256, 2, 2) 918,784 3.7
ResidualConvBlock (8, 256, 2, 2) (8, 512, 1, 1) 3,672,576 3.7
Linear (8, 512) (8, 1) 513 0.0
Total 4,894,049
loss epoch train
0.203 0 train
0.003 0 eval
0.003 1 train
0.003 1 eval
0.003 2 train
0.002 2 eval
0.003 3 train
0.002 3 eval
0.003 4 train
0.002 4 eval 

CPU times: user 16.1 s, sys: 6.03 s, total: 22.1 s
Wall time: 27.6 s
(xb, t) = dls.peek(split="test")
xb, t = xb[:8, ...], t[:8, ...]
t_pred = t_predictor(xb.to(def_device))
titles = [f"True: {tt.item():.2f}, Pred: {tp.item():.2f}" for tt, tp in zip(t, t_pred)]
show_images(xb.squeeze(), titles=titles)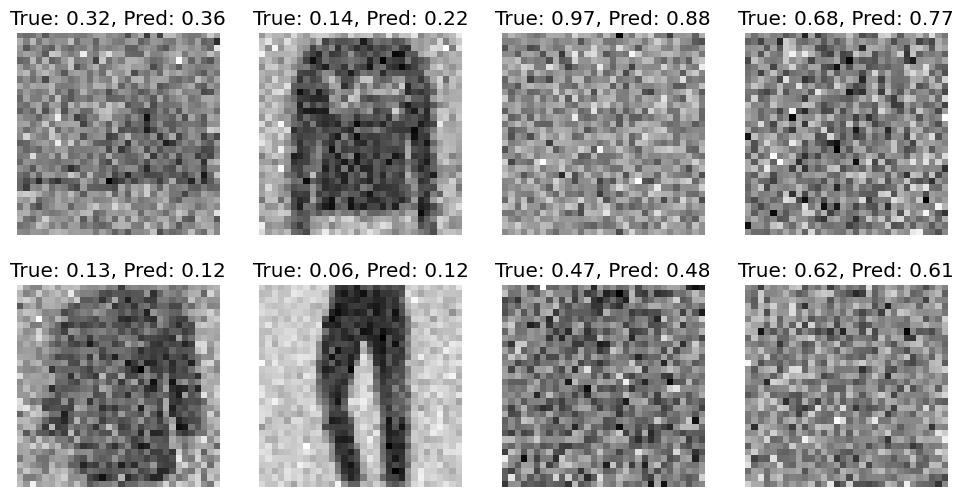

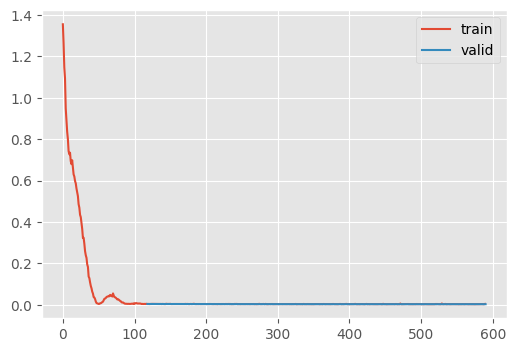
This is worse than what Jeremy reports, but he was using a training batch without augmentation, so he was likely learning the training data directly. Note that Jeremy uses a batch of training data and that our discrepancy is in-line with what we’re getting in the evaluation (unlike Jeremy’s, where the discrepancy is quite large at \(\approx\sqrt{0.08}\).)

with torch.no_grad():
    mse = torch.nn.functional.mse_loss(t_pred.to(def_device), t.to(def_device))
mse
tensor(0.0037, device='cuda:0')

Nice to know that I’m at the point where I can spot bugs in Jeremy’s code 🐛

eval = ImageEval.fashion_mnist(bs=256)

Applying \(t\)-predictor to the diffusion model

At this point, we can add the \(t\) predicting model to the diffusion process.

class ContinuousDDPMWithTPred(ContinuousDDPM):
    @only
    def predict(self, learn):
        (x_t, t), _ = learn.batch
        with torch.no_grad():
            t = t_predictor(x_t).clip(0.01, 0.99)
        learn.preds = learn.model(x_t, t).sample
unet = UNet2DModel(
    sample_size=(32, 32),
    in_channels=1,
    out_channels=1,
    block_out_channels=(16, 32, 64, 128),
    norm_num_groups=8,
)
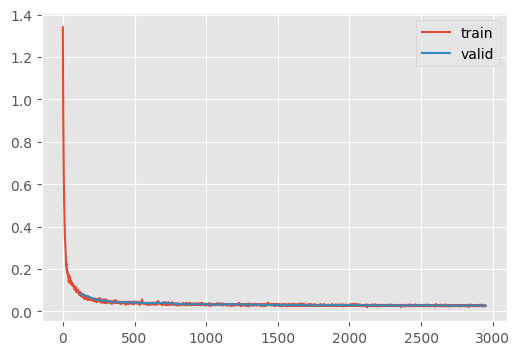
ddpm = ContinuousDDPMWithTPred(βmax=0.01)
train_ddpm(
    unet,
    lr=1e-2,
    n_epochs=25,
    opt_func=partial(torch.optim.Adam, eps=1e-5),
    ddpm=ddpm,
    bs=512,
)
loss epoch train
0.212 0 train
0.085 0 eval
0.064 1 train
0.054 1 eval
0.047 2 train
0.044 2 eval
0.042 3 train
0.042 3 eval
0.040 4 train
0.039 4 eval
0.037 5 train
0.040 5 eval
0.035 6 train
0.034 6 eval
0.034 7 train
0.034 7 eval
0.033 8 train
0.032 8 eval
0.032 9 train
0.034 9 eval
0.031 10 train
0.032 10 eval
0.031 11 train
0.030 11 eval
0.031 12 train
0.030 12 eval
0.030 13 train
0.030 13 eval
0.029 14 train
0.028 14 eval
0.029 15 train
0.030 15 eval
0.029 16 train
0.029 16 eval
0.028 17 train
0.028 17 eval
0.028 18 train
0.028 18 eval
0.028 19 train
0.028 19 eval
0.028 20 train
0.028 20 eval
0.027 21 train
0.028 21 eval
0.027 22 train
0.027 22 eval
0.027 23 train
0.027 23 eval
0.027 24 train
0.027 24 eval 

CPU times: user 10min 1s, sys: 3min 49s, total: 13min 50s
Wall time: 11min 29s

source

ddim_t_pred

 ddim_t_pred (model, sz=(16, 1, 32, 32), device='cpu', n_steps=100,
              eta=1.0, noisify=<function ddim_noisify>)
x_0 = ddim(unet, sz=(256, 1, 32, 32))
show_images(x_0[:8, ...].squeeze(), imsize=1.2)
100%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 99/99 [00:03<00:00, 31.74time step/s]

x_0.min(), x_0.max()
(tensor(-0.5532, device='cuda:0'), tensor(0.6188, device='cuda:0'))
eval.fid(x_0)
147.68310546875

Compare to 789.25 without predicting \(t\) (and 158.81 for a real batch). So, the metrics are much better but it doesn’t look better?