Cosine scheduler, revisited

In this module, we radically simlify the DDPM algorithm by constraining time between 0 and 1

Adapted from

The idea we’ll be exploring is the removing the concept of having \(\frac{t}{T}\)

source

aesthetics

 aesthetics ()

Improve the look and feel of our visualizations

aesthetics()

Often in diffusion, we refer to time steps like so

T = 1000
for t in range(T):
    print(f"Progress: {t/T}")

Jeremy notes that we can simply use a progress variable \(\in [0, 1]\). This allows us to simplify the \(\bar{\alpha}\) expression like so:

source

ᾱ

 ᾱ (t, reshape=True, device='cpu')
x = torch.linspace(0, 1, 100)
plt.plot(x, ᾱ(x, reshape=False));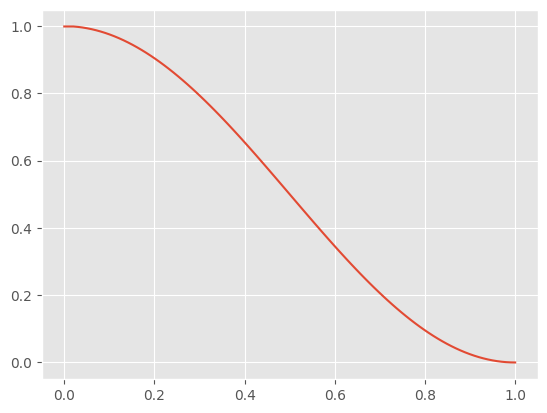

And, furthermore, the noisify function can be simplified like so:

source

noisify

 noisify (x_0, t=None)

Now, (a) we don’t have to deal with knowing the time steps, computing \(\alpha\) and \(\beta\) and (b) the process is continuous.

Let’s add this to the DDPM training callback. Notice that the constructor has been deleted.

source

ContinuousDDPM

 ContinuousDDPM (n_steps=1000, βmin=0.0001, βmax=0.02)

Modify the training behavior

dls = get_dls()
xb, _ = dls.peek()
xb.shape  # Note: 32x32
torch.Size([128, 1, 32, 32])

We can use the parameters from our training run in the previous notebook.

fp = Path("../models/fashion_unet_2x_continuous.pt")
ddpm = ContinuousDDPM(βmax=0.01)
if fp.exists():
    unet = torch.load(fp)
else:
    unet = fashion_unet()
    train(
        unet,
        lr=1e-2,
        n_epochs=25,
        bs=128,
        opt_func=partial(torch.optim.Adam, eps=1e-5),
        ddpm=ddpm,
    )
    torch.save(unet, fp)
f"{sum(p.numel() for p in unet.parameters() if p.requires_grad):,}"
'15,890,753'

To denoise, we need to reverse the noisification. Recall, for a given sample \(x_0\), the noised sample is defined as: x_t = ᾱ_t.sqrt() * x_0 + (1 - ᾱ_t).sqrt() * ε \[ x_t = \sqrt{ \bar{\alpha}_t } x_0 + \left( \sqrt{ 1 - \bar{\alpha}_t } \right) \epsilon \]

Thus,

\[ x_0 = \frac{ x_t - \left( \sqrt{ 1 - \bar{\alpha}_t } \right) \epsilon }{ \sqrt{ \bar{\alpha}_t } } \]

source

denoisify

 denoisify (x_t, noise, t)
(x_t, ts), eps = noisify(xb)
show_images(x_t[:8], titles=[f"{t.item():.2f}" for t in ts[:8]])

This looks impressive for one step, but recall xb is part of the training data.

eps_pred = unet(x_t.to(def_device), ts.to(def_device)).sample
x_0 = denoisify(x_t, eps_pred.cpu(), ts)
show_images(x_0[:8])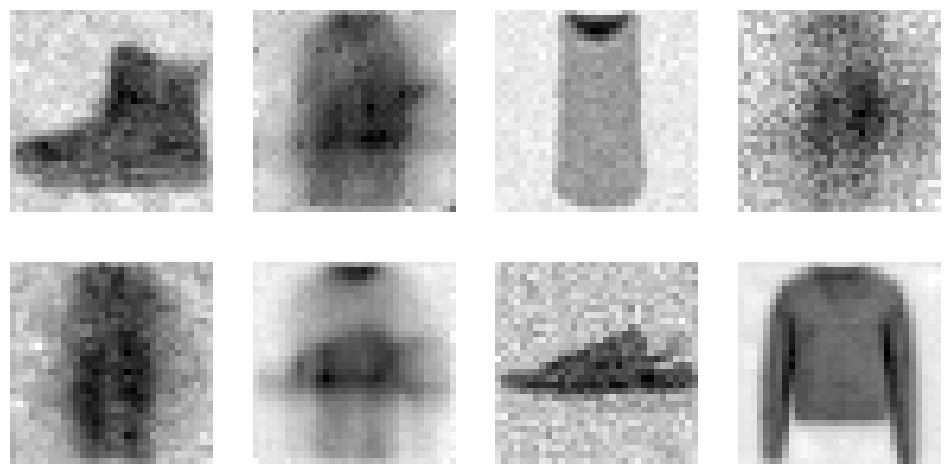

Finally, we can rewrite the sampling algorithm without any \(\alpha\)s or \(\beta\)s. The only function we need is \(\bar{\alpha}_t\), which are part of the noisify and denoisify functions. This also means we can make the sampler a single, elegant function.

source

ddpm

 ddpm (model, sz=(16, 1, 32, 32), device='cpu', n_steps=100)
x_0 = ddpm(unet, sz=(8, 1, 32, 32), n_steps=100)
show_images(x_0, imsize=0.8)
100%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 99/99 [00:01<00:00, 67.69time step/s]

This code had a few bugs in it initially that led to deep-fried results.

  • denoisify was given torch.randn instead of noise_pred
  • The last denoising iteration was given t=1 instead of t=0

Let’s try this with DDIM

source

ddim_noisify

 ddim_noisify (η, x_0_pred, noise_pred, t, t_next)

source

ddim

 ddim (model, sz=(16, 1, 32, 32), device='cpu', n_steps=100, eta=1.0,
       noisify=<function ddim_noisify>)
x_0 = ddim(unet, sz=(8, 1, 32, 32), n_steps=100)
show_images(x_0, imsize=0.8)
100%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 99/99 [00:01<00:00, 70.26time step/s]

bs = 128
eval = ImageEval.fashion_mnist(bs=bs)
x_0 = ddim(unet, sz=(bs, 1, 32, 32), n_steps=100)
eval.fid(x_0)
100%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 99/99 [00:03<00:00, 30.48time step/s]
764.1282958984375

Directly comparing this to DDPM:

x_0 = ddim(unet, sz=(bs, 1, 32, 32), n_steps=100, eta=0.0)  # eta=0 makes this DDPM
eval.fid(x_0)
100%|████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 99/99 [00:03<00:00, 30.55time step/s]
818.5997314453125

and a real batch of data

xb, _ = dls.peek("test")
eval.fid(xb)
158.8096923828125