ResNets

Can we beat 90% accuracy on FashionMNIST?

Adapted from:

set_seed(42)
plt.style.use("ggplot")

Let’s start by cleaning up some of the module implementations.

source

CNN

 CNN (nfs=(8, 16, 32, 64), n_outputs=10, block=None)

6 layer convolutional neural network with GeneralReLU

source

init_leaky_weights

 init_leaky_weights (module)

source

Conv

 Conv (c_in, c_out, stride=2, ks=3, act=True, norm=True)

Convolutional block with norms and activations

source

GeneralReLU

 GeneralReLU (a=0.1, b=0.4)

*Base class for all neural network modules.

Your models should also subclass this class.

Modules can also contain other Modules, allowing to nest them in a tree structure. You can assign the submodules as regular attributes::

import torch.nn as nn
import torch.nn.functional as F

class Model(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = nn.Conv2d(1, 20, 5)
        self.conv2 = nn.Conv2d(20, 20, 5)

    def forward(self, x):
        x = F.relu(self.conv1(x))
        return F.relu(self.conv2(x))

Submodules assigned in this way will be registered, and will have their parameters converted too when you call :meth:to, etc.

.. note:: As per the example above, an __init__() call to the parent class must be made before assignment on the child.

:ivar training: Boolean represents whether this module is in training or evaluation mode. :vartype training: bool*

_, stats = train_1cycle(CNN.kaiming(nfs=(8, 16, 32, 64)))
0.00% [0/3 00:00<?]
79.66% [94/118 00:06<00:01 0.478] 

KeyboardInterrupt

stats.mean_std_plot()

Going deeper

At this point, we can try to go deeper by adding a stride 1 convolution layer

class DeeperCNN(CNN):
    """7 layer convolutional neural network with GeneralReLU"""

    def get_layers(self, nfs, n_outputs=10, C=None):
        if C is None:
            C = Conv
        assert len(nfs) == 5
        # Notice we changed the stride to 1 to fit another layer --+
        layers = [C(1, 8, ks=5, stride=1)]  # 👈 ------------------+
        for c_in, c_out in zip(nfs, nfs[1:]):
            layers.append(C(c_in, c_out))
        layers.append(C(nfs[-1], n_outputs, act=False))
        return layers
train_1cycle(DeeperCNN.kaiming(nfs=(8, 16, 32, 64, 128)));
MulticlassAccuracy loss epoch train
0.783 0.764 0 train
0.818 0.544 0 eval
0.885 0.364 1 train
0.873 0.366 1 eval
0.913 0.271 2 train
0.895 0.314 2 eval

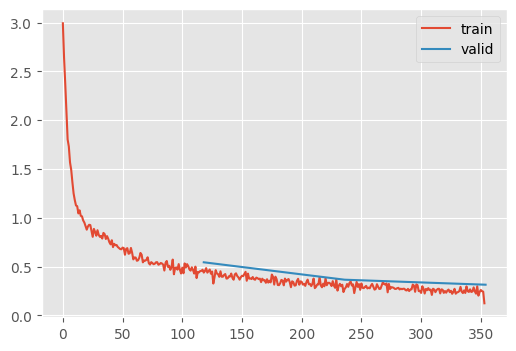
This gives us 90% in 3 epochs, which is the quickest we’ve been able to achieve that accuracy.

We want to make our networks wider and deeper, but this has a limit even with an apropriate initialization. In “Deep Residual Learning for Image Recognition,” Kaiming observed that a 56 layer network had worse performance than a 20 layer network. Why?

Notice, if the 36 extra layers were \(I\), it should have the same performance of the smaller network. In other words, it’s a superset of the small network. We should be able to table advantage of the initial training dynamics of the shallower network with deeper networks with Skip Connections.

class ResidualBlock(nn.Module):
    def __init__(self, inner):
        self.inner = inner

    def forward(self, x):
        x_orig = x
        x = self.inner(x)
        assert x.shape == x_orig.shape
        return x + x_orig

Note that the shape must not change after the inner transformation. To do so with a Convolutional Neural Network, we need a very simple “Identity” convolution that does the same transformation.

F.avg_pool2d?
Docstring:
avg_pool2d(input, kernel_size, stride=None, padding=0, ceil_mode=False, count_include_pad=True, divisor_override=None) -> Tensor
Applies 2D average-pooling operation in :math:`kH \times kW` regions by step size
:math:`sH \times sW` steps. The number of output features is equal to the number of
input planes.
See :class:`~torch.nn.AvgPool2d` for details and output shape.
Args:
    input: input tensor :math:`(\text{minibatch} , \text{in\_channels} , iH , iW)`
    kernel_size: size of the pooling region. Can be a single number or a
      tuple `(kH, kW)`
    stride: stride of the pooling operation. Can be a single number or a
      tuple `(sH, sW)`. Default: :attr:`kernel_size`
    padding: implicit zero paddings on both sides of the input. Can be a
      single number or a tuple `(padH, padW)`. Default: 0
    ceil_mode: when True, will use `ceil` instead of `floor` in the formula
        to compute the output shape. Default: ``False``
    count_include_pad: when True, will include the zero-padding in the
        averaging calculation. Default: ``True``
    divisor_override: if specified, it will be used as divisor, otherwise
         size of the pooling region will be used. Default: None
Type:      builtin_function_or_method

source

ResidualConvBlock

 ResidualConvBlock (c_in, c_out, stride=2, ks=3, act=True, norm=True)

Convolutional block with residual links

m = DeeperCNN.kaiming(nfs=(8, 16, 32, 64, 128), block=ResidualConvBlock)
_ = train_1cycle(m)
MulticlassAccuracy loss epoch train
0.807 0.583 0 train
0.869 0.384 0 eval
0.894 0.289 1 train
0.893 0.288 1 eval
0.926 0.201 2 train
0.915 0.228 2 eval

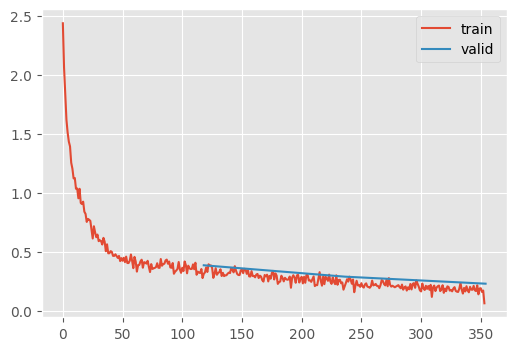
Recall, the previous best was %90.9 after 5 epochs 🥳

Let’s take a closer look at how the parameters are allocated

source

SummaryCB

 SummaryCB (mods=None, mod_filter=<function noop>)

Summarize the model

source

summarize

 summarize (m, mods, dls=<slowai.learner.DataLoaders object at
            0x7f52347e6350>)
for block in [Conv, ResidualConvBlock]:
    print(block.__name__)
    m = DeeperCNN.kaiming(nfs=(8, 16, 32, 64, 128), block=block)
    summarize(m, m.layers)
Conv
Type Input Output N. params MFlops
Conv (512, 1, 28, 28) (8, 28, 28) 216 0.2
Conv (512, 8, 28, 28) (16, 14, 14) 1,184 0.2
Conv (512, 16, 14, 14) (32, 7, 7) 4,672 0.2
Conv (512, 32, 7, 7) (64, 4, 4) 18,560 0.3
Conv (512, 64, 4, 4) (128, 2, 2) 73,984 0.3
Conv (512, 128, 2, 2) (10, 1, 1) 11,540 0.0
Total 110,156 
ResidualConvBlock
Type Input Output N. params MFlops
ResidualConvBlock (512, 1, 28, 28) (8, 28, 28) 1,848 1.4
ResidualConvBlock (512, 8, 28, 28) (16, 14, 14) 3,664 0.7
ResidualConvBlock (512, 16, 14, 14) (32, 7, 7) 14,496 0.7
ResidualConvBlock (512, 32, 7, 7) (64, 4, 4) 57,664 0.9
ResidualConvBlock (512, 64, 4, 4) (128, 2, 2) 230,016 0.9
ResidualConvBlock (512, 128, 2, 2) (10, 1, 1) 13,750 0.0
Total 321,438

Indeed, we have almost 3x as many paramters and the training dynamics are quite stable!

How does this compare to a standard implementation?

def train_timm(id):
    m = timm.create_model(id, in_chans=1, num_classes=10)
    m.layers = []  # Because we're not recording anything
    np = sum(p.numel() for p in m.parameters())
    print(f"N. parameters: {np:,}")
    train_1cycle(m)
train_timm("resnet18")
N. parameters: 11,175,370
MulticlassAccuracy loss epoch train
0.776 0.663 0 train
0.729 0.935 0 eval
0.884 0.312 1 train
0.890 0.316 1 eval
0.914 0.230 2 train
0.906 0.260 2 eval

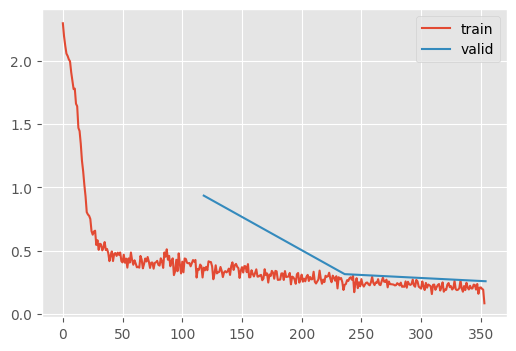
Slightly better! Of course, this model has 30x more parameters, so it’s not surprising.

How does this compare to a network without these links?

class DoubleConvBlock(nn.Module):
    """Convolutional block with residual links"""

    def __init__(self, c_in, c_out, stride=2, ks=3, act=True, norm=True):
        super().__init__()
        self.conv_a = Conv(c_in, c_out, stride=1, ks=ks, act=act, norm=norm)
        self.conv_b = Conv(c_out, c_out, stride=stride, ks=ks, act=act, norm=norm)

    def forward(self, x):
        x = self.conv_a(x)
        x = self.conv_b(x)
        return x
m = DeeperCNN.kaiming(nfs=(8, 16, 32, 64, 128), block=DoubleConvBlock)
shape(m)
0.00% [0/3 00:00<?]
0.00% [0/118 00:00<?]
Type Input Output N. params
DoubleConvBlock (512, 1, 28, 28) (8, 28, 28) 1,832
DoubleConvBlock (512, 8, 28, 28) (16, 14, 14) 3,520
DoubleConvBlock (512, 16, 14, 14) (32, 7, 7) 13,952
DoubleConvBlock (512, 32, 7, 7) (64, 4, 4) 55,552
DoubleConvBlock (512, 64, 4, 4) (128, 2, 2) 221,696
DoubleConvBlock (512, 128, 2, 2) (10, 1, 1) 12,460
Total 309,012 
_ = train_1cycle(m)
MulticlassAccuracy loss epoch train
0.793 0.730 0 train
0.806 0.599 0 eval
0.889 0.348 1 train
0.898 0.304 1 eval
0.920 0.247 2 train
0.910 0.275 2 eval

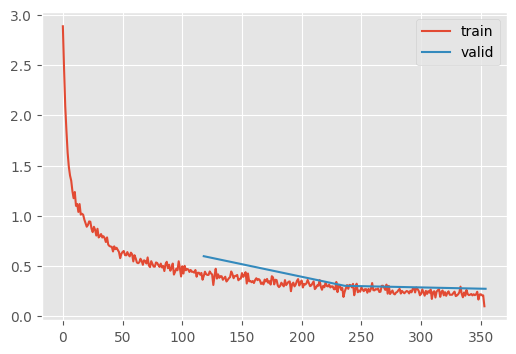
Interestingly, only the slightest bit worse