Diffusion U-Net

Unconditional U-net from scratch

Adapted from

dls = get_fashion_dls(bs=512)

Time embedding

Supposedly, time embeddings are neccesary to achieve modeling high performance

emb_dim = 16

# This was thought to be the longest sequence that a transformer
# should be able to handle, even though nowadays sequences can
# be much longer
max_period = 10_000

print(f"{-math.log(max_period)=}")
exponent = -math.log(max_period) * torch.linspace(0, 1, emb_dim // 2)
plt.plot(exponent);
-math.log(max_period)=-9.210340371976184

They are computed by computing the outer product of the time vector, ts with the exponent function…

bs = 100
ts = torch.linspace(-10, 10, bs)

embedding = ts[:, None].float() * exponent.exp()[None, :]
embedding.shape
torch.Size([100, 8])

note here that, so far, the embeddings aren’t very different

fig, ax = plt.subplots(figsize=(4, 4))
for i in range(0, bs, 25):
    ax.plot(embedding[i], label=f"Timestep #{i+1} Embedding")
ax.set(ylabel="Logit", xlabel="Dimension")
fig.legend();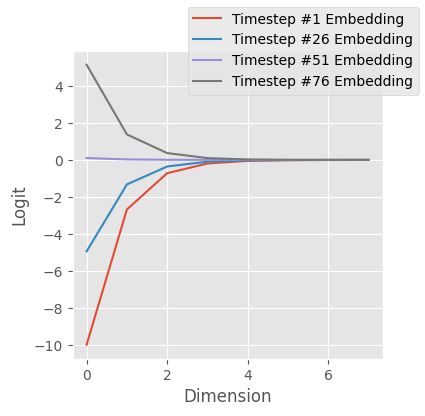

…and projected into cosine and sine space, and then concatenated.

embedding = torch.cat([embedding.sin(), embedding.cos()], dim=-1)
embedding.shape
torch.Size([100, 16])
fig, ax = plt.subplots(figsize=(4, 4))
for i in range(2):
    ax.plot(embedding[:, i], label=f"Sine Dimension #{i+1}")
for i in range(8, 10):
    ax.plot(embedding[:, i], label=f"Cosine Dimension #{i+1}")
ax.set(ylabel="Logit", xlabel="Timestep")
fig.legend();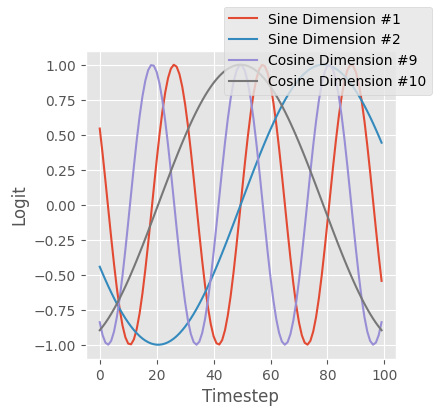

Overall, this results in a time embedding that is similar to its neighbors, but is overall very diverse. This figure demonstrates this, where the first column is similar to the second column, but dissimilar to the 100th column.

show_image(embedding.T);

We can consolidate this.

source

timestep_embedding

 timestep_embedding (ts, emb_dim, max_period=10000)

Editting the number of dimensions increases the column size

show_image(timestep_embedding(ts, 50).T);

Decreasing the max_period increases inter-column heterogeneity.

show_image(timestep_embedding(ts, 16, 100).T);

Let’s reimplement the U-net with time

source

Conv

 Conv (c_in, c_out, ks=3, stride=1)

Wrapper for a Conv block with normalization and activation

source

EmbeddingPreactResBlock

 EmbeddingPreactResBlock (t_embed, c_in, c_out, ks=3, stride=2)

Conv res block with the preactivation configuration

source

SaveTimeActivationMixin

 SaveTimeActivationMixin ()

Helper to save the output of the downblocks to consume in the upblocks

source

TResBlock

 TResBlock (t_embed, c_in, c_out, ks=3, stride=2)

Res block with saved outputs

source

TDownblock

 TDownblock (t_embed, c_in, c_out, downsample=True, n_layers=1)

A superblock consisting of many downblocks of similar resolutions

source

TUpblock

 TUpblock (t_embed, c_in, c_out, upsample=True, n_layers=1)

A superblock consisting of many upblocks of similar resolutions and logic to use the activations of the counterpart downblock.

source

TimeEmbeddingMLP

 TimeEmbeddingMLP (c_in, c_out)

Small neural network to alter the “raw” time embeddings

source

TUnet

 TUnet (nfs=(224, 448, 672, 896), n_blocks=(3, 2, 2, 1, 1),
        color_channels=3)

Diffusion U-net with a diffusion time dimension

source

FashionDDPM

 FashionDDPM ()

Training specific behaviors for the Learner

source

train

 train (model, dls, lr=0.004, n_epochs=25, extra_cbs=[], loss_fn=<function
        mse_loss>)
un = train(
    TUnet(
        color_channels=1,
        nfs=(32, 64, 128, 256, 384),
        n_blocks=(3, 2, 1, 1, 1, 1),
    ),
    dls,
    lr=4e-3,
    n_epochs=25,
)
loss epoch train
0.150 0 train
0.087 0 eval
0.056 1 train
0.054 1 eval
0.046 2 train
0.051 2 eval
0.040 3 train
0.044 3 eval
0.037 4 train
0.044 4 eval
0.035 5 train
0.041 5 eval
0.034 6 train
0.044 6 eval
0.032 7 train
0.037 7 eval
0.031 8 train
0.031 8 eval
0.030 9 train
0.033 9 eval
0.029 10 train
0.035 10 eval
0.029 11 train
0.032 11 eval
0.029 12 train
0.035 12 eval
0.028 13 train
0.030 13 eval
0.028 14 train
0.028 14 eval
0.027 15 train
0.028 15 eval
0.027 16 train
0.029 16 eval
0.027 17 train
0.027 17 eval
0.026 18 train
0.027 18 eval
0.026 19 train
0.027 19 eval
0.026 20 train
0.027 20 eval
0.026 21 train
0.026 21 eval
0.026 22 train
0.025 22 eval
0.026 23 train
0.026 23 eval
0.025 24 train
0.026 24 eval 

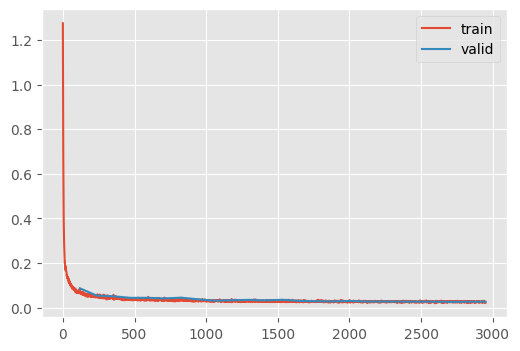
CPU times: user 13min 10s, sys: 24.9 s, total: 13min 34s
Wall time: 13min 42s
xb, _ = dls.peek()
xb.shape
torch.Size([512, 1, 32, 32])
n_steps = 100
ts = torch.linspace(1 - (1 / n_steps), 0, n_steps).to(xb.device)
x_t = torch.randn(16, 3, 64, 64)

source

ddpm

 ddpm (model, sz=(16, 1, 32, 32), device='cpu', n_steps=100)
x_0, _ = ddpm(un, (8, 1, 32, 32))
show_images(x_0, imsize=0.8)
100%|████████████████████████████████████████████████████████████| 99/99 [00:00<00:00, 145.43time step/s]

This is not bad! This achieves a similar performance to the Huggingface implementation with a simliar number of parameters.